The wave function for the electron in an atom must be normalized (or at least normalizable). Therefore,
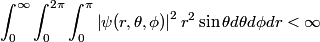 The wave function is presumably separable into an angular part and a radial part. So, this inequality becomes 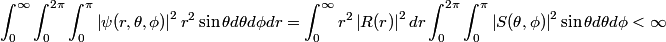 In order for the product of two numbers to be finite, both numbers must be finite. So, 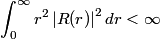 If 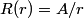 or or 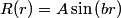 , then clearly this inequality is not satisfied. Therefore, the wavefunctions II and III could not possibly be the radial wavefunctions for an electron in an atom. On the other hand, if , then clearly this inequality is not satisfied. Therefore, the wavefunctions II and III could not possibly be the radial wavefunctions for an electron in an atom. On the other hand, if 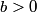 , then , then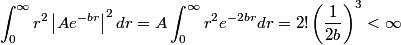 Therefore, wave function I is normalizable. That does not necessarily mean it is the radial wave function for an electron in an atom. But in fact the radial wave function for an electron in the ground state hydrogen is 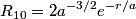 where  is the Bohr radius. (See Griffiths QM page 154.) is the Bohr radius. (See Griffiths QM page 154.)Therefore, wave function I could and DOES represent the radial wave function for an electron in an atom. Therefore, answer (A) is correct. |